Accelerometri e vibrazioni: la Guida
Come valutare i dati misurati sugli altoparlanti, come tradurli in pressione emessa? Come valutare un buon cabinet e quanto deve durare la vibrazione? Nessuno ve ne ha mai parlato perché quelli che scrivono tanta teoria spesso mancano di un elemento basilare: l’esperienza acquisita sul campo...
Negli ultimi anni la disponibilità degli accelerometri a basso costo è aumentata notevolmente e molti, vista la relativa facilità di utilizzo, ne hanno approfittato per arricchire il proprio laboratorio. L’accelerazione - lo abbiamo studiato a scuola - rappresenta la variazione di velocità rispetto al tempo che passa. Se sono lanciato con la mia auto ad 80 chilometri l’ora e resto a questa velocità in maniera costante, possiamo dire che la mia accelerazione vale esattamente zero, proprio perché non è né aumentata né diminuita. Una ripresa bruciante, diciamo da zero a 100 km/h in 2,8 secondi, rappresenta una accelerazione notevole perché in 2,8 secondi la velocità varia da zero a 100 km/h.
Ai maniaci dei calcoli ricordo che per ottenere un risultato corretto si deve prima cambiare la velocità da chilometri orari in metri al secondo (dividendo i km/h per 3,6) e poi fare il calcolo, giusto per ottenere un 'g' di accelerazione. Già, perché nel nostro sistema di grandezze l’accelerazione si esprime in m/s2 (metri al secondo quadrato) che diviso 9,80665 (valore 'convenzionale' di 'g' in m/sec2 come media dei valori ai poli e all'equatore) ci fornisce l’accelerazione in 'g', ovvero l’accelerazione espressa in gravità, quella che possiede un corpo che cade da una certa altezza al suolo. Ma torniamo a noi ed agli accelerometri. In buona sostanza un accelerometro è un sensore che genera una tensione direttamente proporzionale alla variazione della velocità nel tempo, ovvero alla accelerazione della superficie alla quale è reso solidale.
Per effettuare misure quanto meno credibili è necessario conoscere la tensione di uscita dal sensore quando questo è sottoposto ad una accelerazione di un g. Vi ricordo che 1 g equivale a 9,80665 m/s2 (metri al secondo quadrato) che è l’unità di misura corretta nel sistema MKS che usiamo per convenzione. Per conoscere il valore di tensione dell’accelerometro occorre una sorgente nota con una certa precisione, un po’ come i generatori di una pressione nota che usiamo per calibrare i microfoni. I calibratori per gli accelerometri pur se tutto sommato banali nel loro funzionamento, hanno un pregio ed un difetto. Il pregio è che ci indicano con precisione l’accelerazione che generano così da poter calibrare il nostro sensore, mentre il difetto è costituito, tanto per cambiare, dal costo.
In vero devo dire che sui sensori di accelerazione anche abbastanza economici quasi sempre è indicato il valore di tensione per un g in maniera abbastanza precisa, cosa che ho verificato su diversi ACH-01 che ho dovuto calibrare per diversi colleghi. In generale gli accelerometri che funzionano sul principio piezoelettrico offrono una tensione di uscita molto bassa, con al massimo una decina di millivolt per un g. Ovvio che oltre a dover fornire una tensione di polarizzazione, come per i microfoni ad elettrete, è necessaria una notevole amplificazione che a seconda del tipo di accelerometro può andare da 20 a 40 dB, come a dire da 10 a 100 volt per ogni volt di ingresso. Personalmente ho adottato un sistema abbastanza semplice, ovvero quello di amplificare l’accelerometro con due operazionali in cascata, con uno solo dei due a guadagno regolabile, così da avere un volt di uscita per ogni g ed avere automaticamente 1v/1g e poter leggere direttamente l’accelerazione sulla scala delle tensioni della scheda di misura.

A sinistra un ACH-01; a destra il B&K 4393
Le prime problematiche che si presentano quando cerchi di usare un accelerometro per fare le misure di vibrazione sulle pareti del diffusore o direttamente sulla membrana di un altoparlante per misurarne l’accelerazione sono sostanzialmente due: come incollare in maniera estremamente rigida il sensore sulla superficie da misurare e come tenere conto della massa del sensore, specialmente quando occorre connettere il sensore alla membrana di un altoparlante, visto che la sua massa fa corpo unico e quindi si somma a quella della membrana stessa.
Sugli altoparlanti di diametro contenuto ciò può rappresentare un problema. Il mio B&K 4393 pesa, senza l’apporto del sottile cavo, appena 1,5 grammi mentre il più massiccio ACH-01 pesa un po’ di più, circa 2,3 grammi, sempre avendo cura di non aggiungere una porzione di cavo al peso sulla bilancia. Possiamo decidere allora che già un midwoofer da una ventina di grammi di massa mobile possa essere misurato con una buona precisione. Il fissaggio del sensore appare una operazione più complessa. E’ sempre possibile incollare il sensore sulla superficie da misurare con una goccia di colla cianoacrilica, ma specialmente per le membrane degli altoparlanti il bello viene quando occorre staccare il sensore dopo aver effettuato la misura!
Per i tweeter il problema è appena diverso, visto che si può utilmente fissare il sensore direttamente sulla flangia frontale, in genere avvitata abbastanza rigidamente al complesso magnetico, a patto che il sensore possieda una banda passante sufficientemente estesa. La cosa vi permette anche di scoprire quanto questo trasduttore vibri, trasmettendo la sua vibrazione direttamente al mobile che lo ospita, rispetto ad un midwoofer di medie dimensioni (diciamo da 100 mm di diametro in su). Torniamo al fissaggio del sensore. La soluzione più intuitiva sarebbe quella di fissarlo col doppio adesivo.
Questa soluzione, specialmente se l’adesivo è gommoso, perde parte della sua validità appena oltre i 250-300 Hz rappresentando un tramite troppo cedevole. Ho scovato, dopo approfondite indagini in tutte le cartolerie della mia città, un doppio adesivo della marca 'Tesa' molto sottile e rigido, e pure molto coriaceo. L’accelerazione misurabile supera bellamente i 3 kHz senza perdita alcuna. Ne ho in laboratorio un rotolone, sufficiente ad incollare sensori per un centinaio di anni! Poi ci sono sostanze più semplici da reperire che funzionano molto bene ma che lasciano un segno indelebile sulla membrana ed anche sui box, così che la loro scelta dipende da quanti danni ci possiamo permettere nelle nostre indagini.
Facciamo due calcoli.
In regime sinusoidale l’escursione, la velocità lineare, la velocità di volume e l’accelerazione sono legate da semplici equazioni:
u0 = ws x Xrms (rms)
Ovvero la velocità lineare della membrana è legata all’escursione Xrms ed alla pulsazione ovvero w = 2 x Pg x f, mentre la velocità di volume, che si esprime con la u maiuscola vale:
U0 = SD x u0 (rms)
dove SD rappresenta l’area effettiva della membrana = Pg x ra2 oppure Pg x D2/4
dove Pg rappresenta il pigreco (3,141592…), ra rappresenta il raggio della membrana dell’altoparlante e D rappresenta il diametro (in MKS si usano metri e metri quadrati)
L’accelerazione arms si calcola da:
arms = uo x ws,
oppure, per quanto visto prima,
arms = ws x ws x X0 = ws2 x X0
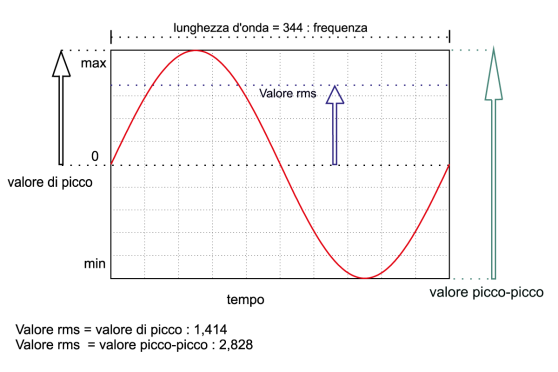
A questo punto occorre una piccola precisazione, che se ignorata conduce ad errori notevoli. Avrete notato il pedice rms che sta a significare che il valore della grandezza è espressa in valore quadratico medio (Root Mean Square) che nel segnale sinusoidale, e solo in questo, obbedisce alle semplici equazioni:
Xrms = Xpp/(2√2)
Ovviamente Xpp sta per x picco/picco ovvero, in una sinusoide, da picco positivo a picco negativo, mentre
Xp = Xrms x √2.
Xp sta per escursione di picco, con (2√2) che vale 2,8284 e √2 che vale 1,4142.
Per farci una idea possiamo dare uno sguardo alla figura qui in alto dove si può notare il valore rms, quello di picco ed il valore picco picco di una sinusoide, qualunque sia la grandezza rappresentata. Ora, parlando di escursioni della membrana o di una parete del diffusore che vibra sia la grandezza picco/picco che la grandezza espressa in rms ci interessano relativamente perché usiamo in genere il valore rms soltanto per il calcolo della pressione generata. L’escursione della membrana infatti ci interessa quando è vicina al suo limite di picco, col valore picco/picco che è meno facilmente relabile alla pressione emessa, anche se spesso la misura picco/picco è foriera, come vedremo, di sorprese notevoli.
Partiamo da lontano…
La pressione della 'mitica' sfera pulsante vale:
[1] P = U0 x ρ x f / (2 x r)
Dove la pressione P è espressa in Pascal, ovvero in Newton/m2, ρ è la densità dell’aria, che nel nostro caso vale 1,21 Kg/m3 e r rappresenta la distanza dell’ideale microfono di misura.
Da quanto fin qui visto abbiamo che
[2] U0 = D2 x Pg/4 x arms/ws
Inserendo la [2] nella [1] ad un metro di distanza del microfono (r=1) otteniamo:
Prms = D2 x Pg/4 x arms/ws x ρ x f
con la pressione, ovviamente, espressa in Pascal.
Semplificando abbiamo che
Prms= arms x ρ/8 x D2
Siamo praticamente giunti al punto che ci interessa, ovvero risalire dall’accelerazione misurata in m/s2 alla pressione emessa. Una aggiustatina alla formula, con conseguente espressione in decibel ci consente di scrivere:
[3] P(dB) = 77,573 + 20 log10 (D2 x arms)
I 77,573 dB equivalgono, ovviamente, a 20 Log10 (ρ/8/0,00002), con 0,00002 che è la pressione di riferimento Pref ovvero 20 micropascal. Vi faccio notare che l'accelerazione è sempre espressa in m/s2 e che può essere convertita in g con la formula: a(g) = arms / 9,807, oppure, ribaltando la formula, arms = a(g) x 9,807. La formula ottenuta [3] appare per noi abbastanza importante. Innanzitutto la misura di accelerazione effettuata su un altoparlante, con 2,83 vrms ai morsetti, ci conduce direttamente alla pressione emessa o, se ribaltiamo la formula, la pressione emessa e misurata magari con precisione, ci conduce al valore di accelerazione della membrana a quella frequenza con la formula inversa:
arms = 10 [(spl-77,573)/20] /D2
Un esempio di misura
Poniamo di avere sul tavolo un woofer caratterizzato da 172 millimetri di diametro, che in metri diventano 0,172 metri. Sottoposto ad una tensione di 2,83 v alla frequenza di risonanza, ovvero 30 Hz tondi tondi, rilevo a rms = 13 g che moltiplicati per 9,807 danno 127,49 m/s2. La pressione emessa dal woofer sarà allora:
P = arms x D2 x (ρ/8) = 127,49 x 0,02958 x 0,151 =0,5695 Pa
che convertiti in dB conducono alla pressione di 89,08 dB, che poi è stata effettivamente confermata dal microfono di misura. Per non avere nessun punto oscuro in questa spiegazione dirò che per convertire 0,569 Pascal si divide questa pressione per Pref, se ne fa il logaritmo in base 10 e poi si moltiplica per 20, ovvero:
Press(dB) = 20 x log10 (Pascal/0,00002)
La misura delle vibrazioni
Nel caso invece della misura delle vibrazioni delle pareti del mobile occorre un po’ di ragionamento ed un po’ di pratica. Si, direte voi, ma quanto deve valere l’accelerazione di una parete di un diffusore per poter dire che il cabinet è stato realizzato bene e, soprattutto, questa vibrazione quanto tempo deve durare, e che andamento nel tempo deve avere? Prima di snocciolare numeri a casaccio sono andato a guardare nel mio archivio storico ed ho notato che in effetti c’è un ampio range di variazione tra i peggiori ed i migliori mobili prodotti. Cerchiamo di non commettere errori di misura e di conseguenza di non fare errori di valutazione.
Teoricamente possiamo risalire dall’accelerazione alla pressione emessa dal mobile di un diffusore misurando con l’accelerometro la parete laterale e la parete frontale, giusto per verificare quanta colorazione aggiungono. Vi faccio notare che la pressione emessa dal cabinet è difficile da misurare da sola con un microfono. Andiamo però a vedere dal punto di vista meccanico cosa stiamo misurando. Ponendo il sensore di accelerazione al centro, ad esempio, della parete laterale noi misureremo una sorta di membrana bloccata a tutte le estremità, col centro che esprime la massima sollecitazione alle deformazioni. Ovvio che non è un valore probante in assoluto.
La parete in quel punto sta esprimendo il suo massimo, e per ottenere un dato interessante dovremmo suddividere il pannello laterale in quadrati, ad esempio, di 2,5 – 3 centimetri, eseguire un sacco di misure e poi fare la media dei valori misurati. Ho provato questa lunga sequenza di misure più di una volta ed ho ottenuto sempre risultati coerenti con la divisione dell’area del pannello per 2,5. Nella nostra formula dall’area del pannello ricaviamo il diametro equivalente da inserire nella [3] in questo modo:
[4] Dequiv = 0,713 x SQR(Sparete)
Dove S= D2 x Pg/4, e S/2,5 =Deq2 x Pg/4 e D =SQR [4/(2,5 x Pg) x S]
Dove SQR rappresenta l’operazione di radice quadrata. La base e l’altezza della parete vanno computati (in metri!) però non sulla dimensione esterna ma su quella interna perché nelle giunzioni e nelle incollature il pannello ovviamente è quasi del tutto fermo. Vediamo di effettuare qualche misura che ci chiarisca le idee.
Facciamo qualche esempio…
Prendiamo un diffusore di dimensioni molto contenute, circa 5 litri, realizzato con un medium density da 25 millimetri molto economico. Il tweeter ha la cupola da 29 millimetri ed il magnete in neodimio, mentre il woofer ha 87 millimetri di membrana ed un magnete in ferrite. Per entrambi gli altoparlanti non ho usato filtri crossover ma ho allungato verso l’esterno i cavi di connessione, così che posso cambiare velocemente il trasduttore da collegare all’amplificatore che emette rigorosamente 2,83 volt rms.
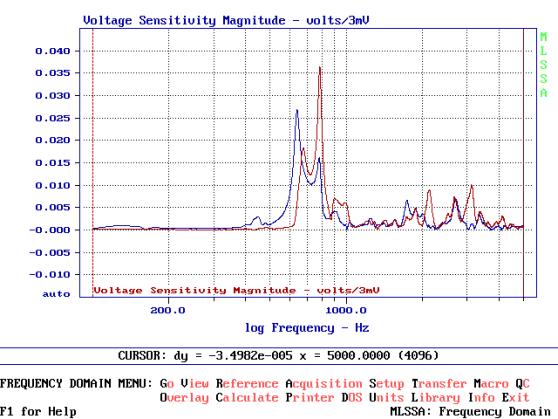
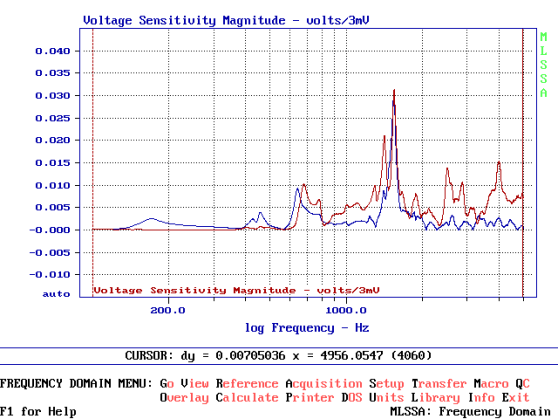
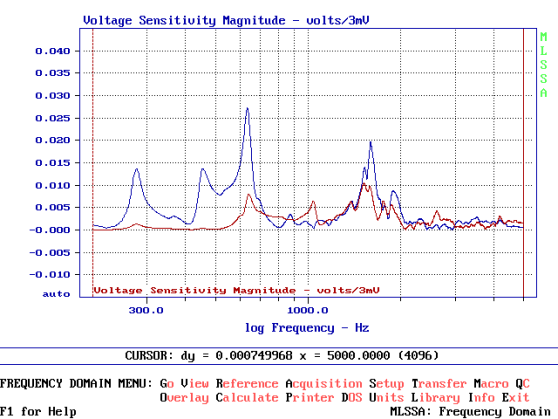
L’accelerometro è fissato esattamente al centro della parete laterale destra. Nel grafico 2.0 possiamo vedere direttamente la misura fatta da MLSSA con il setup che ho realizzato espressamente per la misura dell’accelerazione. Notate in alto la dicitura volts/3mV che in realtà è l’abbreviazione di 3,16 mV e serve ad ottenere 1 volt per g. La curva rossa rappresenta l’apporto del tweeter e la curva blu quello del woofer. Il picco di accelerazione del tweeter vale poco più di 0,035 g mentre quello del woofer non arriva a 0,025 g. Notate ancora che il tweeter ha una guarnizione morbida mentre il woofer è fissato direttamente al pannello frontale. Cosa possiamo vedere?
Innanzitutto vediamo che il tweeter mette in vibrazione la parete laterale molto più del woofer. In seconda battuta notiamo che la risonanza a 786 Hz, presente in entrambe le misure, è da attribuire al materiale usato, che si produce in più di una risonanza, ma con la fondamentale che vale ben 0,037 g, ovvero .362 m/s2. Logica vorrebbe che per un buon diffusore occorra assolutamente cambiare fornitore di mdf o richiedere un materiale migliore, più smorzato. Ora grazie all’accelerometro ed a questo articolo abbiamo anche un elemento di valutazione capace di farcene rendere conto molto velocemente.
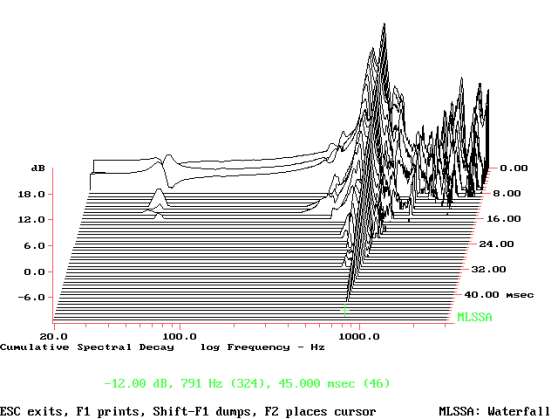
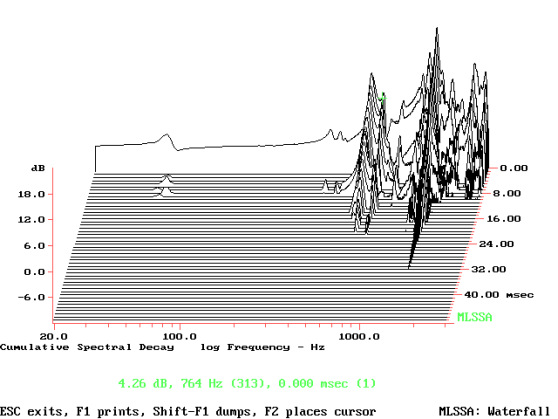
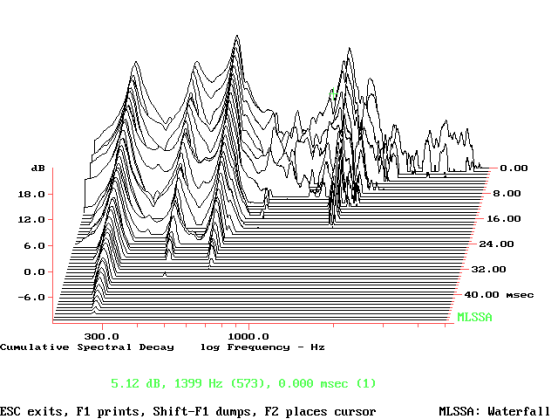
Nel grafico 2.1 possiamo vedere la waterfall delle accelerazioni del solo tweeter. Notiamo come la risonanza del materiale duri oltre 40 millisecondi, come a dire che il suono emesso percorre ancora ben 13,7 metri. La superficie della parete laterale misurata internamente (oppure esternamente decurtando la misura di due volte lo spessore del materiale usato) vale 20 x 25 centimetri, ovvero 500 cm2 ovvero, ancora, 0,05 metri quadri. Dividendo questa grandezza per 2,5 (una operazione che come sappiamo è empirica) otteniamo il diametro equivalente di 0,159 metri, come se si trattasse di un woofer da 16 cm di diametro. Inserendo questo dato nella [3] otteniamo che
Prms = 77.573 + 20 log10 (0,1592 x 0,362) = 36,8 dB
che non rappresenta un dato pessimo, specialmente se a 87 dB di pressione media a 2,83 vrms, i 36,8 dB non superano il livello della seconda e della terza armonica che lo stesso trasduttore emette e che, ovviamente, ho misurato. Il non grande valore del trasduttore mi porta comunque a pensare che la pressione delle vibrazioni ora calcolata sia da considerarsi eccessiva, specialmente in una porzione della gamma media alla quale siamo ben sensibili. Oltretutto nella waterfall vediamo che i primi millisecondi della risonanza della parete mantengono un livello elevato, anche se la rappresentazione è espressa in ampiezza con i decibel e non in modo lineare, come sarebbe il caso dell’accelerazione. Procediamo nella nostra indagine.
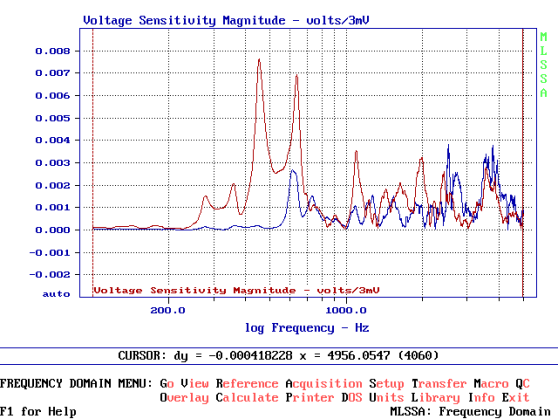
Nel grafico 3.0 possiamo vedere le vibrazioni del pannello frontale. Nella curva rossa vediamo il tweeter e nella curva blu vediamo le risonanze provocate dal solo woofer. Il sensore è stato posizionato esattamente al centro tra i due trasduttori.
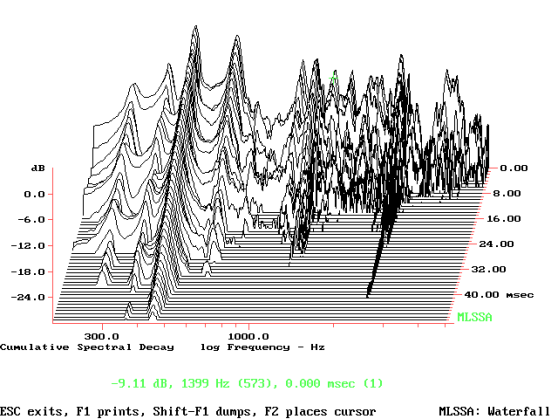
Nel grafico 3.1 possiamo notare come anche la waterfall del tweeter appaia molto pulita, con una durata del decadimento della risonanza di “soli” 32 millisecondi. Notate ancora un paio di differenze: intanto la risonanza del pannello, pur con un accenno ai 786 Hz visti prima ora sale decisa a 1544 Hz, una frequenza quasi doppia rispetto a quella vista prima. Oltre a ciò notate come le due accelerazioni, quella provocata dal woofer e quella “istigata” dal tweeter, quasi si equivalgano al picco di risonanza, ma con valori decisamente minori. “Ma come” - direte voi - “si tratta della parete frontale, quella più critica”! E invece tocca contraddirvi, perché in questo caso, come in tutte le realizzazioni attente, abbiamo la parete frontale fissata “sopra” le pareti laterali così che si trova sollecitata “a taglio” e risulta di fatto molto più rigida. Si tratta di un piccolo trucco istigatomi nei primi anni ’90 da Joseph Szall, credo.
Con le stesse modalità viste prima andiamo a verificare quanta pressione emette la sola parete frontale. La parete frontale misura 10 x 25 centimetri, per un’area di 0,025 metri quadrati. Il diametro equivalente di questa parete grazie alla [4] vale 0,112 metri quadri, che immessi nella [3] assieme all’accelerazione misurata ci conducono ad una pressione abbastanza modesta. Passiamo ora ad un box di dimensioni più che triple, realizzato con un mdf più sordo. Nel grafico qui in basso possiamo vedere la misura delle vibrazioni rilevate al centro del pannello laterale. Notate come le risonanze del materiale siano spostate ad una frequenza più bassa rispetto a prima e come i due woofer da 110 millimetri di diametro possiedano una maggiore capacità di trasmettere vibrazioni rispetto al tweeter.
Notate anche come al picco abbiamo misurato una accelerazione notevolmente minore, ovvero 0,0044 g, quasi un decimo rispetto a quella vista prima, cosa che testimonia la bontà del materiale scelto. Base ed altezza della parete valgono 42 x 26 centimetri, ovvero 0,1196 metri quadrati che secondo la [4] equivalgono ad un diametro di 246 millimetri. Immettendo questa grandezza nella [3] otteniamo una pressione rms di….24,6 dB, ovvero molto poco, visto che a 90 dB la seconda armonica è stata trovata ad un livello medio di -42 dB rispetto alla fondamentale. La distorsione quindi ha un livello di pressione quasi 10 volte maggiore di quella prodotta dalla vibrazione. Ma non è tutto oro quello che luccica.
Il grafico qui in alto ci mostra infatti come la waterfall sia addirittura più 'lunga' di 40 millisecondi, anche se visto il basso livello della misura MLSSA ha aggiornato, per mantenere costante la dinamica, il fondo del grafico a -30 dB. Trascurabile dunque? Credo di si. Certo che la cosa si fa interessante!
Nel grafico qui in alto vediamo le accelerazioni misurate sul frontale, disponendo l’accelerometro nelle vicinanze del tweeter. Possiamo ancora notare come l’accelerazione di colore blu dovuta ai due woofer sia maggiore dell’emissione del tweeter. Con un diametro equivalente di 0,162 metri otteniamo una pressione emessa di 30,3 dB, un dato ancora di ottimo livello.
Nel grafico qui in alto vediamo la waterfall dei due woofer che ha il decadimento peggiore a circa 280 Hz, ove si allunga fino a circa 48 millisecondi. Nel grafico precedente però notiamo che il picco di ampiezza maggiore è posizionato a circa 633 Hz. Occhio quindi che alle ampiezze maggiori non sempre corrisponde una maggior durata nel tempo. Questa vibrazione, come possiamo vedere, si smorza in un tempo relativamente breve. Dopo appena 18,7 millisecondi il decadimento è maggiore di 20 dB, un dato che unito alla bassa pressione emessa finisce per scomparire sul fondo del grafico.
Il box più grande
Per il terzo esempio sono passato ad un diffusore storico ma decisamente più grosso, con un volume interno di circa 60 litri ed un woofer da 12 pollici. Il box al suo interno ha dei rinforzi perimetrali che hanno la particolarità di non toccarsi tra loro, come si fa nella costruzione di molti strumenti musicali. Purtroppo posso soltanto misurare le vibrazioni totali, visto che il proprietario quando ha sentito la mia richiesta di smontare il crossover per misurare le azioni di ogni singola via… non mi è sembrato molto contento.
Prima di misurare le vibrazioni del cabinet occorre dire che il woofer da 232 millimetri di diametro è fissato con otto solide viti con tanto di madrevite annegata nel pannello frontale. Occorre anche aggiungere che la guarnizione messa dal proprietario, troppo morbida, è stata eliminata, mentre il midrange ed il tweeter non sono stati toccati. Come vediamo in foto (foto 3) l’accelerometro è stato fissato al centro della parete laterale, che misura 22,5 x 59,5 centimetri, equivalenti, dopo i soliti calcoli, ad un diametro equivalente di 260 mm.
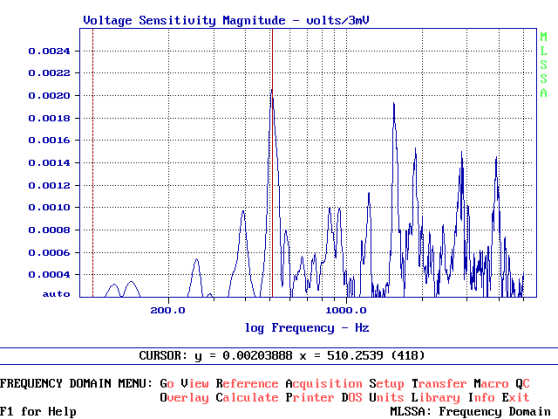
Nel grafico qui in alto possiamo vedere quanto siano ridotte le vibrazioni del diffusore, che sarà stato sgamato dagli appassionati, e che non è realizzata in mdf ma in vero legno. Notiamo come le risonanze del legno siano distribuite su un intervallo contenuto ma siano ben visibili, a differenza del medium density che sparpaglia le risonanze su un intervallo più vasto. I calcoli soliti effettuati ci conducono a calcolare che il picco massimo, centrato a 510 Hz emette una pressione di circa 20 dB, poca cosa in verità per un diffusore di queste dimensioni, con un diametro equivalente abbastanza esuberante.
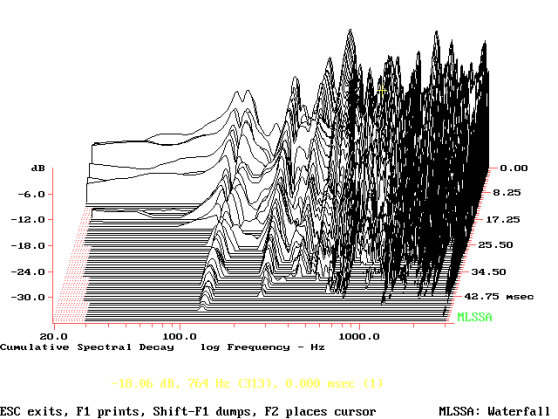
In questo ultimo grafico vediamo la waterfall. Questo grafico ci dice che a 128 Hz si superano, anche se di poco, i 42 millisecondi anche se con un decadimento abbastanza veloce. Ciò equivale a dire che sia per il legno che per il medium density un buon tempo della durata della vibrazione sia, appunto, 40-45 millisecondi.
Conclusioni
Abbiamo visto come misurare, con una discreta precisione, la pressione emessa dalle pareti del diffusore disponendo di un economico accelerometro e di qualche formula ben calibrata. Potremmo estrapolare il valore dello spostamento della membrana del woofer, ma credo che lo spazio che mi concede il “Frattacapo” stia esaurendosi. Appena avrò un po’ di tempo metterò la matita sul foglio per estrarre l’escursione, così da camuffare un accelerometro in un laser micrometrico, certamente più costoso. La presenza nel mio laboratorio di un laser di spostamento mi confermerà la precisione del calcolo e della misura. Stay tuned!
Similar Post You May Like
-
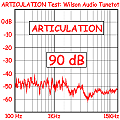
Misure: l'articulation test di Gian Piero Matarazzo
Una misura non facile da pensare, da effettuare e da rendere automatica, stabile ed a prova... »
-

Diffusore acustico: 4 gradini delle prestazioni
Esistono dei criteri oggettivi per definire la qualità di un diffusore? Noi crediamo di si,... »
-
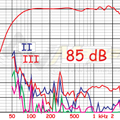
Diffusori: impedenza e distorsione
Le misure, croce e delizia del tecnici che devono effettuarle e dei lettori meno tecnici che... »
-
Diffusori: tempo e frequenza
Le misure, croce e delizia del tecnici che devono effettuarle e dei lettori meno tecnici che... »
-

Diffusori: introduzione alle misure
Una volta le misure sui diffusori venivano descritte come una sorta di "magia", realizzata... »
Commenti (2)
-
27 Luglio 2023, 10:20
Accelerometri e vibrazioni: la Guida
complimenti per l'articolo! è bello leggere che la fisica si applica anche al mondo dell'audio...a leggere alcuni brani sembra che invece obbedisca a leggi differenti! -
27 Luglio 2023, 15:06
Accelerometri e vibrazioni: la Guida
Ammetto di non aver seguito l'articolo parola per parola, ammesso di riuscirci (e ne dubito) mi mancano troppe nozioni per dare un peso effettivo agli aspetti più strettamente tecnici.
Credo di aver capito che il metodo di misurazione proposto si prefigga lo scopo di arrivare ad una precisione comparabile con quella ottenibile in un laboratorio dotato di laser micrometrico (di cui solo ora apprendo l'esistenza nei laboratori di elettroacustica ad una frazione del costo. E' così?
Credo anche di aver capito che che la misura consenta, se il sensore è applicato al cabinet, di misurarne le vibrazioni, e quindi di inferirne in qualche modo il contributo di questo alla sonorità della cassa. E' abbastanza chiaro anche il discorso sullo smorzamento anche se il risultato non dovrebbe essere troppo diverso da quello misurabile con un microfono e comunque (sbaglio?) dovrebbe dipendere anche dal damping e quindi dall' amplificatore usato (???).
(@runner: comunque sì, l'acustica è uno dei capitoli del gran libro della fisica)